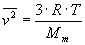
Temperature of a gas is basically the speed with which the gas molecules move. If a gas (the kinetic fuel) hits a space craft at a given speed, this speed can therefore be related to an equivalent temperature. This is what I will do here.
All physical formulas and constants used can be found in my old school formulary, so it is pretty basic stuff.
Average squared speed of a molecule of an ideal gas is
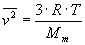
where T is the temperature
in Degree Kelvin,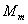 
is the molar mass of
the gas and 
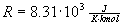is the gas constant.
The average squared speed of the molecules is not the same as the squared average speed of particles, but due to the Maxwell speed distribution the relation is
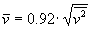, which means 
.
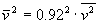Molar mass related to the mass of a gas particle is
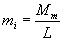, where 
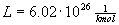is Avogadros constant.
Mass of a molecule is easier described by the number of neutrons and protons per molecule (atomic weight of a molecule) with
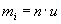, where n
is the atomic weight and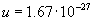 
is the weight of a proton
or neutron.
Now putting these formulas together we get:
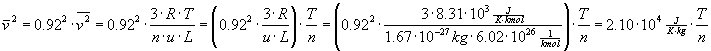
Calling the combined constants Q,
we get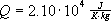 
and:
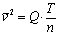
So finally the temperature equivalent of a gas moving at speed v with an atomic molecular weight of n is
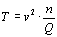
At re-entry of a space shuttle from low earth orbit, speed of the gas is about 8 km/s. Air consists of nitrogen and oxygen molecules, which have an atomic weight of 28 and 32. We can approximate this by 30 and get a temperature of the thin air hitting the aerobrake of
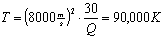
which is 90 thousand degree Celsius!!!
When a capsule from the moon enters earth atmosphere with a speed of 11.2 km/s, it even encounters a temperature equivalent of 180 thousand degrees Celsius.
One really wonders how an aerobrake can survive such temperatures. And it tells us that care must be taken on how to design the aerobrake for inverted aerobraking. Whatever makes a normal aerobrake survive these temperatures must be duplicated for the inverted aerobrake.
It might be worth noting that hydrogen has a much lower temperature equivalent than oxygen, water or any other possible fuel (see figure 1). Therefore it seems to be an ideal choice of fuel. But note also that a space shuttle needs a heat shield to re-enter earths atmosphere anyway, so maybe the effort needed to bring liquid hydrogen from outer space will not be worth the reduced complexity and weight of the inverted aerobrake. On the other hand side, anything much heavier than oxygen will most likely not be a good choice of kinetic fuel for normal inverted aerobraking. But in case significant amounts of on-board fuel are heated up by the extraterrestrial fuel to achieve additional thrust (and cool the aerobrake), heavier fuels should be considered too.
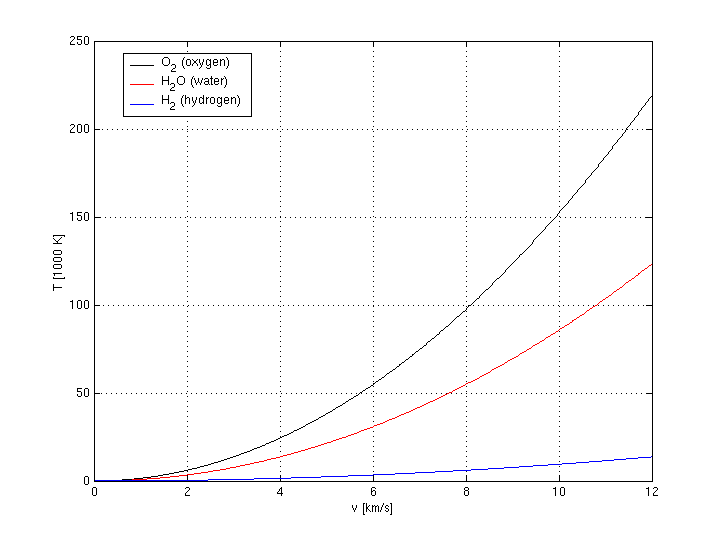
Figure 1: Equivalent temperature in thousand degrees Kelvin (and degrees Celsius) of different fuels moving at a speed of v kilometer per second.
As a final remark: there probably are differences between a cloud of gas molecules moving in the same direction and a cloud of gas molecules moving at the same average speed, but at random directions. An analogy may be laser light, which is very much like ordinary light. But sometimes it exhibits special properties (e.g. you can create holograms). The same may be true for gas: equivalent temperature may not always mean the same thing as ordinary temperature.
Another way to ask for an equivalent temperature of fast moving gas would be: how hot would the gas become, if the gas is stopped and all of its kinetic energy is converted into thermal energy?
Average kinetical energy of a gas molecule in an ideal gas with temperature T:
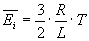
Kinetical energy of a gas molecule at speed v is:
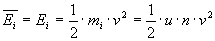
Solving this gives
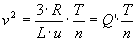
with Q' = 24800. This is quite similar to Q = 21000 from above. With this way of estimating, equivalent temperature is about 15% less.
We would have arrived at the same result above, if we would have asked: what is the temperature of a gas, in which the molecules have the same average squared velocity as the squared velocity of the kinetic fuel?